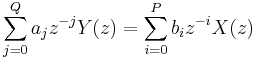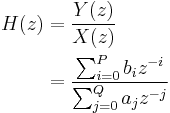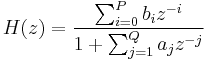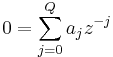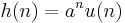Infinite impulse response
Infinite impulse response (IIR) is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time. This is in contrast to finite impulse response (FIR) filters, which have fixed-duration impulse responses. The simplest analog IIR filter is an RC filter made up of a single resistor (R) feeding into a node shared with a single capacitor (C). This filter has an exponential impulse response characterized by an RC time constant.
IIR filters may be implemented as either analog or digital filters. In digital IIR filters, the output feedback is immediately apparent in the equations defining the output. Note that unlike FIR filters, in designing IIR filters it is necessary to carefully consider the "time zero" case in which the outputs of the filter have not yet been clearly defined.
Design of digital IIR filters is heavily dependent on that of their analog counterparts because there are plenty of resources, works and straightforward design methods concerning analog feedback filter design while there are hardly any for digital IIR filters. As a result, usually, when a digital IIR filter is going to be implemented, an analog filter (e.g. Chebyshev filter, Butterworth filter, Elliptic filter) is first designed and then is converted to a digital filter by applying discretization techniques such as Bilinear transform or Impulse invariance.
Example IIR filters include the Chebyshev filter, Butterworth filter, and the Bessel filter.
Contents |
Transfer function derivation
Digital filters are often described and implemented in terms of the difference equation that defines how the output signal is related to the input signal:
where:
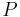 is the feedforward filter order
is the feedforward filter order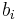 are the feedforward filter coefficients
are the feedforward filter coefficients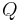 is the feedback filter order
is the feedback filter order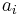 are the feedback filter coefficients
are the feedback filter coefficients![\ x[n]](/2012-wikipedia_en_all_nopic_01_2012/I/d12f3dea01e8dbdf2e162193a66cd85a.png) is the input signal
is the input signal![\ y[n]](/2012-wikipedia_en_all_nopic_01_2012/I/40b136445985b3ab52376234ac90de3d.png) is the output signal.
is the output signal.
A more condensed form of the difference equation is:
which, when rearranged, becomes:
To find the transfer function of the filter, we first take the Z-transform of each side of the above equation, where we use the time-shift property to obtain:
We define the transfer function to be:
Considering that in most IIR filter designs coefficient 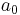 is 1, the IIR filter transfer function takes the more traditional form:
is 1, the IIR filter transfer function takes the more traditional form:
Description of block diagram
A typical block diagram of an IIR filter looks like the following. The 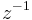 block is a unit delay. The coefficients and number of feedback/feedforward paths are implementation-dependent.
block is a unit delay. The coefficients and number of feedback/feedforward paths are implementation-dependent.
Stability
The transfer function allows us to judge whether or not a system is bounded-input, bounded-output (BIBO) stable. To be specific, the BIBO stability criteria requires that the ROC of the system includes the unit circle. For example, for a causal system, all poles of the transfer function have to have an absolute value smaller than one. In other words, all poles must be located within a unit circle in the  -plane.
-plane.
The poles are defined as the values of  which make the denominator of
which make the denominator of 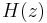 equal to 0:
equal to 0:
Clearly, if 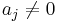 then the poles are not located at the origin of the z-plane. This is in contrast to the FIR filter where all poles are located at the origin, and is therefore always stable.
then the poles are not located at the origin of the z-plane. This is in contrast to the FIR filter where all poles are located at the origin, and is therefore always stable.
IIR filters are sometimes preferred over FIR filters because an IIR filter can achieve a much sharper transition region roll-off than FIR filter of the same order.
Example
Let the transfer function of a filter H be
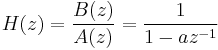 with ROC
with ROC 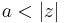 and
and 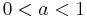
which has a pole at a, is stable and causal. The time-domain impulse response is
which is non-zero for 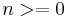 .
.
Applications
The main advantage IIR filters have over FIR filters is that through recursion they use fewer taps. Therefore in digital signal processing applications IIR filters use fewer computing resources than an equivalent FIR filter. A disadvantage of IIR filters is they can be unstable and subject to limit cycle behavior.
See also
- Autoregressive model
- Electronic filter
- Finite impulse response
- Recurrence relation, mathematical formalization
- System analysis
External links
- The fifth module of the BORES Signal Processing DSP course - Introduction to DSP
- IIR Digital Filter Design applet in Java
- IIR Digital Filter design tool - produces coefficients, graphs, poles, zeros, and C code
![\begin{align}
y[n] & = \frac{1}{a_{0}}(b_{0} x[n] %2B b_{1} x[n-1] %2B \cdots %2B b_{P} x[n-P] \\
& - a_{1} y[n-1] - a_{2} y[n-2] - \cdots - a_{Q} y[n-Q])
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/4ff8ef7c59e3ab5e9dd69d4b3dd37f52.png)
![\ y[n] = \frac{1}{a_{0}} \left(\sum_{i=0}^P b_{i}x[n-i] - \sum_{j=1}^Q a_{j} y[n-j]\right)](/2012-wikipedia_en_all_nopic_01_2012/I/68bdd6431e6c3e15e6c44c43f06dad1f.png)
![\ \sum_{j=0}^Q a_{j} y[n-j] = \sum_{i=0}^P b_{i}x[n-i]](/2012-wikipedia_en_all_nopic_01_2012/I/a3d4e7b5805403309d5f4ef2ef86ba29.png)